Smoothing Indicators like MA(), EMA(), T3(), DEMA(), etc. are intended to give you an average indication of price movements. They do this by filtering out high frequency changes in a particular price variable. The problem is that such indicators introduce time lag into the system. Indicator lag is most readily apparent when the overall price chart is relatively smooth (for example, when a simple MA() stays within the High-Low range), and suddenly the price shifts or gaps. When this happens, most smoothing indicators need many bars to overcome the influence of these gaps and re-position themselves back within the average price range of the bar.
Although all trading systems depend on lag to know that something has changed, the degree of lag needed by a system varies. Resettable indicators are most useful in systems that require a smoothing function that closely follows the price, i.e., one that exhibits a minimum of lag.
When a Resettable Indicator encounters a sudden larger-than-normal offset to the average price, it changes behavior and resets the Indicator to a calculated reference point. While there are other patterns or conditions (Signals, Stops, Targets, etc.) in which you might want to reset an Indicator, this discussion focuses on simple gaps that are defined by the AFL functions GapUp() and GapDown(). The techniques introduced here work equally well with EOD or RT data. Another application of the concept would be in RT trading where you might want to reset your Indicator at the start of each new day or trading session.
The reset idea is based on the fact that smoothing functions have a primary period and that the Indicator’s lag will be proportional to that period, i.e. longer periods increase lag and shorter periods decrease lag. Knowing that, we can reset an Indicator by simply setting its period to a lower value. Typically, resetting to a period of 1 works fine. After the reset bar, the period is increased with each passing bar until it has reached its original value.
Consider the EOD example shown below. White bars identify the Gaps that trigger a reset.
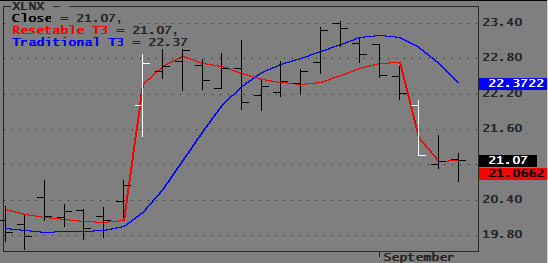
At the first White bar the price gaps up and the Traditional T3 (Blue) falls behind immediately and actually moves opposite to the price. The Resettable T3 (Red) reset itself when it detected the gap and almost immediately is able to track the price bars in the right direction.
There are many ways to reset an indicator: you can do it abruptly by setting the period to 1; you can maintain a minimum smoothing by resetting it to 2 or 3; or you can gradually adjust period and/or T3-Sensitivity according to some formula. The example code below uses the T3 formula that can be found in the AmiBroker library.
In the example below, I use the start (1st bar) of the trading day to reset the T3. However, there are many other situations where you might want to reset an indicator. For example, when using trailing stops or SAR type exits, sometimes you might want to reset an indicator when you get a Buy or Sell signal. You can assign your own reset reference by averaging all bar prices, e.g., (O+H+L+C)/4. However, you should stay away from averaged values as they would reintroduce lag. I prefer the use of (O+C)/2, but you should try any number of other ideas that fit your liking.
function T3( Price, T3Periods, s )
{
e1 = AMA( Price, 2 / (T3Periods+1));
e2 = AMA( e1, 2 / (T3Periods+1));
e3 = AMA( e2, 2 / (T3Periods+1));
e4 = AMA( e3, 2 / (T3Periods+1));
e5 = AMA( e4, 2 / (T3Periods+1));
e6 = AMA( e5, 2 / (T3Periods+1));
C1 = -s^3;
C2 = 3*s^2*(1+s);
C3 = -3*s*(s+1)^2;
C4 = (1+s)^3;
T3Result= c1*e6+c2*e5+c3*e4+c4*e3;
return T3Result;
}
function T3r( C, T3Sensitivity, T3Periods, ResetReference )
{
global Reset;
CPrice = IIf(Reset, ResetReference, C );
T3Periods = Min( T3Periods, BarsSince(Reset));
T3Periods = IIf(Reset,1, T3Periods );
s = T3Sensitivity;
e1 = AMA( CPrice, 2 / (T3Periods+1));
e2 = AMA( e1, 2 / (T3Periods+1));
e3 = AMA( e2, 2 / (T3Periods+1));
e4 = AMA( e3, 2 / (T3Periods+1));
e5 = AMA( e4, 2 / (T3Periods+1));
e6 = AMA( e5, 2 / (T3Periods+1));
C1 = -s^3;
C2 = 3*s^2*(1+s);
C3 = -3*s*(s+1)^2;
C4 = (1+s)^3;
T3Result= c1*e6+c2*e5+c3*e4+c4*e3;
return T3Result;
}
T3Sensitivity = Param("T3 Sensitivity",1,0.1,5,0.01);
T3Periods = Param("T3 Periods",3,1,10,1);
Reset = GapUp() OR GapDown();
ResetReference = (H+L+C)/3;
T3rPlot = T3r( C, T3Sensitivity, T3Periods, ResetReference );
Plot(C,"\nClose",IIf(Reset,2,1),128);
Plot(T3rPlot,"\nResetable T3",4,1|styleThick);
Plot(T3( C, T3Periods, T3Sensitivity),"\nTraditional T3",6,1|styleThick);
Edited by Al Venosa
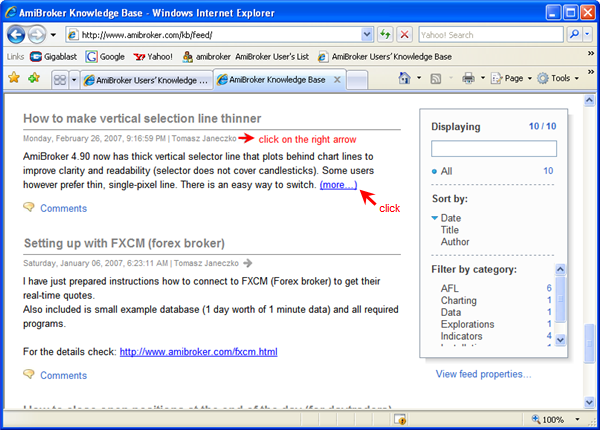
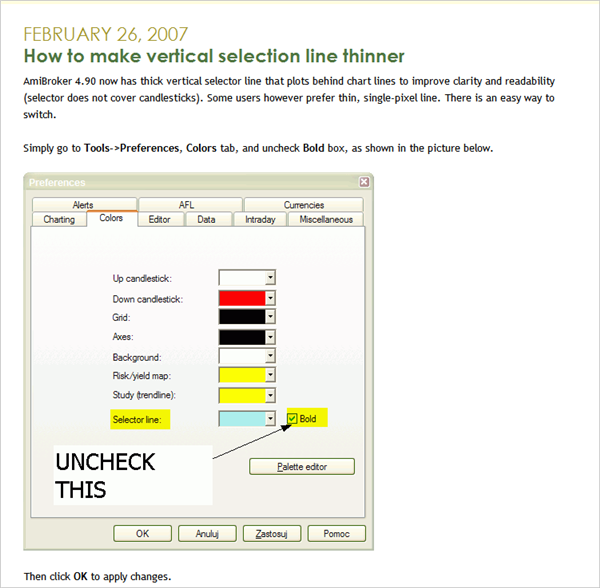
 Filed by brian_z at 1:05 pm under RSS Feeds
Filed by brian_z at 1:05 pm under RSS Feeds